Zana's Mathematics Blog

BLOG MATEMATIKA

KELAS 8 : BAB 6 LINGKARAN

D. Sudut Pusat dan Sudut Keliling Lingkaran.


  1. Hubungan Sudut Pusat dan Sudut Keliling.

     Sudut pusat adalah sudut yang dibentuk oleh dua jari-jari lingkaran yang berpotongan di titik pusatnya. Adapun Sudut keliling adalah sudut yang dibentuk oleh dua tali busur yang berpotongan di satu titik pada keliling lingkaran.

Contoh: 

Seperti gambar di atas, OA dan OB berpotongan di O membentuk sudut pusat, yaitu /_AOB ( sudut AOB). Adapun tali busur AC dan CB berpotongan di titik C membentuk sudut keliling /_ACB (sudut ACB).

NOTE:

 Jadi, sudut pusat <AOB dan sudut keliling <ACB menghadap busur yang sama, yaitu AB dan jika sudut pusat dan sudut keliling menghadap busur yang sama maka besar sudut pusat = 2 x besar sudut keliling.

2. Besar Sudut Keliling yang Menghadap Diameter Lingkaran.

     Pada contoh gambar di atas, ruas garis CB adalah diameter lingkaran. Karena <CAB (sudut CAB) adalah sudut keliling yang menghadap diameter CB, maka besar <ACB = 90 derajat.

  3. Sudut-Sudut Keliling yang Menghadap Busur yang Sama.

     Sudut ABE, ACE, dan ADE adalah sudut keliling yang menghadap AE. Sedangkan pada gambar tersebut <AOE (sudut AOE) adalah sudut pusat yang menghadap AE.

NOTE :

Besar sudut-sudut keliling yang menghadap

busur yang sama adalah sama besar atau

1/2 x sudut pusatnya.

# Contoh Soal :  

 Perhatikan gambar. 

Diketahui: Jika <AOB = 70 derajat.

Ditanya   : Maka <ACB berapa?

Jawab     : <ACB = 1/2 x <AOB

                            = 1/2 x 70 derajat

                            = 35 derajat.

E. Segi Empat Tali Busur ( Pengayaan ).

  1. Pengertian Segi Empat Tali Busur.

     Segi empat tali busur adalah segi empat yang titik-titik sudutnya terletak pada lingkaran.

  

  2. Sifat-Sifat Segi Empat Tali Busur.

     # Sifat-sifat yang dimiliki oleh segi empat tali busur tersebut adalah :

>Pada gambar di atas tampak bahwa sudut-sudut yang berhadapan pada segi empat tali busur ABCD 

  /_ABC dengan /_ADC dan /_BAD dengan /_BCD

> Jumlah 2 sudut yang saling berhadapan pada segi empat tali busur adalahh 180 derajat.

     #Selanjutnya, ada banyak macam-macam segi empat tali busur antara lain : 

*Segi empat tali busur yang salah satu diagonalnya merupakan diameter lingkaran disebut segi empat tali busur siku-siku.

*Segi empat tali busur yang kedua diagonalnya merupakan diameter lingkaran akan membentuk bangun  persegi panjang.

*Segi empat tali busur yang kedua diagonalnya merupakan diameter lingkaran yang saling berpotongan tegak lurus akan membentuk bangun persegi.

F. Sudut Antara Dua Tali Busur ( Pengayaan )

  1. Sudut Antara Dua Tali Busur Jika Berpotongan di Dalam 

      Lingkaran.

     # Besar sudut antara dua tali busur yang berpotongan di dalam lingkaran sama dengan setengah dari jumlah sudut-sudut pusat yang menghadap busur yang diapit oleh kaki-kaki sudut itu.

     # Rumus menurut gambar di atas adalah : 

        <AED = 1/2 x ( <AOD + <BOC )

  2. Sudut Antara Dua Tali Busur yang Berpotongan di Luar 

      Lingkaran.

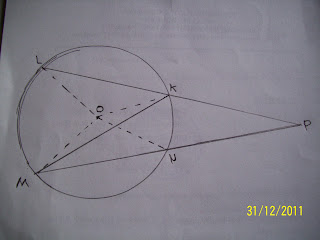
     * Besar sudut antara dua tali busur yang berpotongan di luar lingkaran sama dengan setengah dari selisih sudut-sudut pusat yang menghadap busur yang diapit oleh kaki-kaki sudut itu.

     * Rumus menurut gambar di atas adalah : 

        <KPN = 1/2 x ( <MOL - <KON )

# Contoh Soal : 

 Perhatikan gambar.

Diketahui : <LPM = 25 derajat.

                 <KON = 35 derajat.

Ditanya    : Tentukan besar /_LOM.

Jawab      : <LPM = 1/2 x ( <LOM - <KON )

                 25 derajat = 1/2 x ( <LOM - 35 derajat )

                 50 derajat = <LOM - 35 derajat

                 <LOM = 85 derajat.